Showcase
Showcase
Optimizing geometrical accuracy by curved mesh elements
Achieving a precise geometrical representation in numerical simulations typically involves refining mesh elements around curved areas of the geometry. However, this traditional method results in increased memory usage due to the greater number of elements involved.
Utilizing polynomials to curve elements to the geometry is a common strategy for enhancing geometrical resolution. Yet, the accuracy of this approach hinges on the degree of the polynomial; insufficient degrees lead to subpar geometrical resolution, even with adaptive mesh refinement techniques.
Our innovative approach involves enriching the initial mesh with the original geometrical data. By leveraging the parametric description of the geometry, we directly interpolate and curve each element to conform precisely to the geometry. Unlike polynomial-based methods, our approach ensures an exact representation of the geometry at every refinement level.
The GIF is a demonstration of this geometry interpolation algorithm in action, showcasing curved tetrahedral mesh elements conforming to an airplane geometry while a refinement plane of level 2 moves along the aircraft's axis.
In benchmark tests conducted on a workstation (768 GB RAM) with 100 parallel processes, we achieved remarkable results. Without visualization output, our algorithm processed up to 5.6 billion tetrahedra, with load-balancing taking a mere 7 seconds thanks to the exceptional efficiency of our t8code technology.
Exceeding 1 Trillion mesh elements
To demonstrate the exceptional efficiency of t8code, we used the full JUWELS supercomputer (ca. 100k processes) to create and manage a massive mesh of 1.1 Trillion elements. In this examples we used a hybrid mesh of hexahedra, tetrahedra and prisms. Even with such large numbers, t8code only takes seconds to perform parallel mesh management tasks: Computing the Ghost layer was done in 1.4 seconds and load-balancing in 0.3.
For more details see our paper on a Ghost algorithm for hybrid meshes.
Generating pictures using png2mesh
The png2mesh library can convert .png images into adaptive meshes. In order to do so, it uses the t8code library to build a mesh and refine it at the positions of dark pixels in the original image. You can choose between a quad mesh, triangle mesh, or a hybrid mesh containing both shapes. For more details see the png2mesh github page.
In this example our t8code logo was used to generate an adaptive mesh. On the left side, a hybrid mesh with a maximal level of 7 was used. On the right side, the logo was converted with a transparent background using a quad mesh.
Our submissions to the International Meshing Roundtable (IMR) 2022
The International Meshing Roundtable 2022 was held as part of the SIAM Conference on Parallel Processing for Scientific Computing 2022 (PP22). Following their call for entries to the meshing contest IMR, we constructed this mesh of the famous Seattle Space Needle. Our submission demonstrates the capability of t8code to manage very large hybrid meshes.
The mesh representing the Space Needle is embedded into a cubic mesh made out of all supported 3D mesh elements (hex, tets, prisms and pyramids).
Every element of the cubic mesh that intersects a line of the Space Needle mesh is refined - producing 81 million elements in 11.6 seconds on 56 cores. The mesh also visualizes the huge difference in size that elements can have. On the coarsest level the elements have a diameter of up to 10m while the finest level divides the elements into elements that are 2cm small.
Have a look at our other submissions to the SIAM PP22:
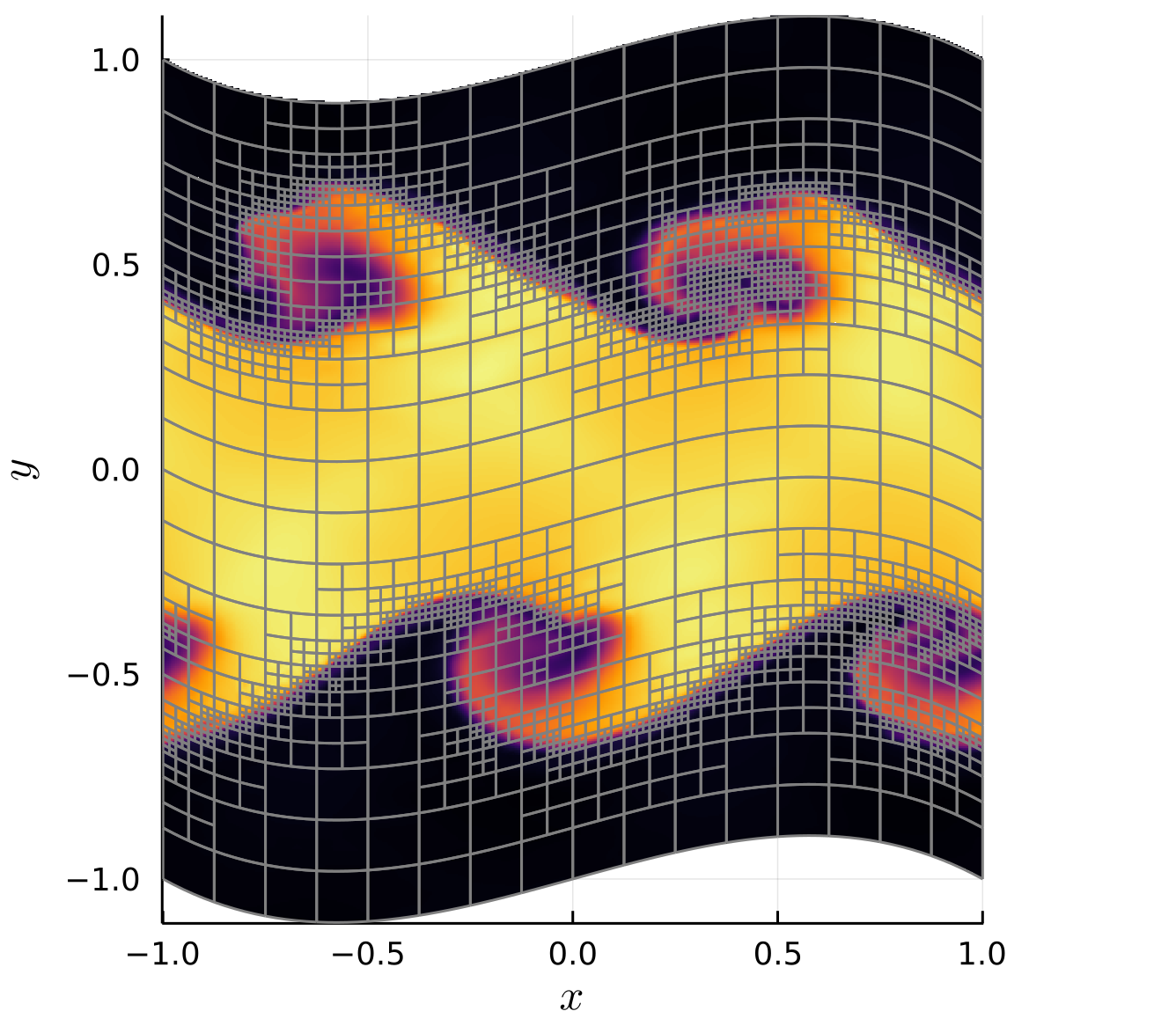
Collaboration with Trixi.jl - a numerical simulation framework for hyperbolic conservation laws written in Julia
Trixi.jl is a numerical simulation framework for a huge variety of hyperbolic conservation laws and is written in Julia . Key objective is to pave the way for dynamical-adaptive, hybrid, curvilinear meshes in Trixi.jl by interfacing with t8code. Scalable management of hybrid meshes - the combination of different element types (triangles, quadrilaterals, tetraeders, hexaeders, pyramids, etc.) into one single datastructure - is a unique feature of t8code, which is not provided by other meshing libraries. Hybrid meshes allow for a flexible and robust high-order approximation of complex geometries typically found in many engineering applications. The project is still work-in-progress.